Mundarija:
Video: Gauss eliminatsiyasi yordamida chiziqli tenglamani qanday yechish mumkin?
2024 Muallif: Miles Stephen | [email protected]. Oxirgi o'zgartirilgan: 2023-12-15 23:41
Tenglamalar tizimini yechish uchun Gauss eliminatsiyasidan qanday foydalanish kerak
- Har qanday qatorni ko'paytirishingiz mumkin tomonidan doimiy (noldan tashqari). uchinchi qatorni ko'paytiradi tomonidan -2 sizga yangi uchinchi qatorni berish uchun.
- Har qanday ikkita qatorni almashtirishingiz mumkin. birinchi va ikkinchi qatorlarni almashtiradi.
- Ikki qatorni birga qo'shishingiz mumkin. bir va ikkinchi qatorlarni qo‘shib yozadi ichida ikkinchi qator.
Keyin, Gaussni yo'q qilish qanday ishlaydi?
Ochig'ini aytganda, Gaussni yo'q qilish ishlari yuqoridan pastga, eshelon shaklida matritsa hosil qilish uchun, holbuki Gauss - Iordaniya bartaraf etish qaerda davom etadi Gauss keyin qisqartirilgan eshelon shaklida matritsa hosil qilish uchun pastdan yuqoriga ishlamasdan qoldi. Texnika quyidagi misolda tasvirlanadi.
Bundan tashqari, Kramer qoida matritsalari nima? Kramer qoidasi 2 × 2 tizim uchun (ikki o'zgaruvchi bilan) Kramer qoidasi determinantlar yordamida chiziqli tenglamalar tizimini yechishning yana bir usuli hisoblanadi. Belgilar nuqtai nazaridan, a matritsa while kvadrat qavslar ichiga olingan raqamlar massivi aniqlovchi ikkita vertikal chiziq bilan o'ralgan raqamlar massivi.
Ikkinchidan, Gaussni yo'q qilishning maqsadi nima?
Gaussni yo'q qilish . Vikipediyadan, bepul ensiklopediya. Gaussni yo'q qilish , shuningdek, qatorni qisqartirish deb ham ataladi, chiziqli tenglamalar tizimini echish uchun chiziqli algebrada algoritmdir. Odatda koeffitsientlarning tegishli matritsasi bo'yicha bajariladigan operatsiyalar ketma-ketligi tushuniladi.
Gauss va Gauss Jordanni yo'q qilish o'rtasidagi farq nima?
3 ta javob. Gaussni yo'q qilish matritsani satr eshelon shaklida qo'yishga yordam beradi, esa Gauss - Iordaniyani bartaraf etish matritsani kichraytirilgan qatorli eshelon shaklida qo'yadi. Kichik tizimlar uchun (yoki qo'lda), odatda foydalanish qulayroqdir Gauss - Iordaniyani yo'q qilish va har bir ifodalangan o'zgaruvchi uchun aniq hal qiling ichida matritsa tizimi.
Tavsiya:
Kvadrat tenglamani nol faktorlar qonuni yordamida qanday yechish mumkin?
Bundan shunday xulosa chiqarishimiz mumkin: Agar har qanday ikkita sonning ko'paytmasi nolga teng bo'lsa, u holda raqamlarning biri yoki ikkalasi ham nolga teng. Ya'ni, agar ab = 0 bo'lsa, u holda a = 0 yoki b = 0 (bu a = b = 0 bo'lish imkoniyatini o'z ichiga oladi). Bu null faktor qonuni deb ataladi; va biz kvadrat tenglamalarni yechish uchun tez-tez foydalanamiz
Chiziqli tenglamalar tizimini grafik usulda qanday yechish mumkin?
Chiziqli tenglamalar sistemasini grafik usulda yechish uchun ikkala tenglamaning grafigini bir xil koordinatalar tizimida tuzamiz. Tizimning yechimi ikkita chiziq kesishgan nuqtada bo'ladi. Ikkala chiziq (-3, -4) da kesishadi, bu tenglamalar tizimining echimi hisoblanadi
Chiziqli tengsizliklar va chiziqli tenglamalarni yechish qanday o'xshash?
Chiziqli tengsizliklarni yechish chiziqli tenglamalarni yechishga juda o‘xshaydi. Asosiy farq shundaki, siz manfiy songa bo'lish yoki ko'paytirishda tengsizlik belgisini aylantirasiz. Chiziqli tengsizliklarni grafikda ko'rsatishda yana bir nechta farqlar mavjud. Soyalangan qism chiziqli tengsizlik to'g'ri bo'lgan qiymatlarni o'z ichiga oladi
Chiziqli tengsizlik tenglamasini qanday yechish mumkin?
Uch qadam bor: Tenglamani shunday o'zgartiringki, "y" chap tomonda, qolgan hamma narsa o'ngda. 'y=' chizig'ini chizing (uni y≤ yoki y≥ uchun qattiq chiziq va y uchun kesik chiziq qilib qo'ying) "kattaroq" (y> yoki y≥) uchun chiziq ustidagi yoki chiziq ostidan soya qiling. 'kichikroq' (y< yoki y≤)
O'zgaruvchini ajratib olish orqali tenglamani qanday yechish mumkin?
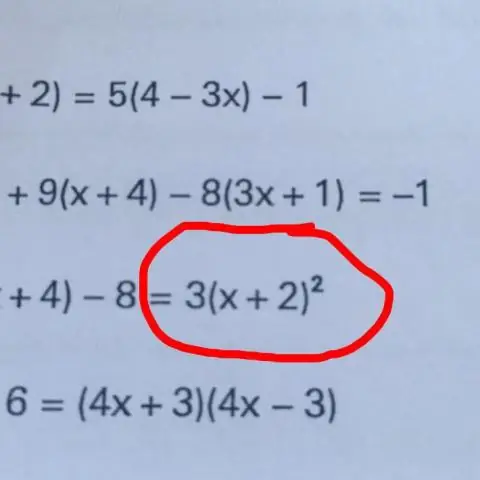
O'zgaruvchini ajratib olishning asosiy usuli bu tenglamaning "ikki tomoniga ham biror narsa qilish", masalan, tenglamaning ikkala tomonini bir xil raqamga qo'shish, ayirish, ko'paytirish yoki bo'lish. Ushbu jarayonni takrorlash orqali biz tenglamaning bir tomonida ajratilgan o'zgaruvchini olishimiz mumkin