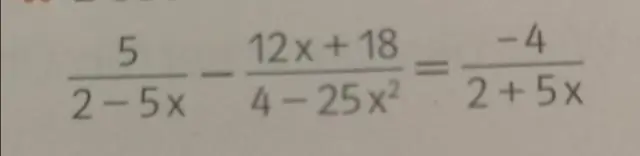
- Muallif Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:41.
- Oxirgi o'zgartirilgan 2025-01-22 17:13.
THE BURCHLAR METODI Mumkin bo'lgan to'plam (mintaqa) grafigi, S. toping Barcha uchlarning aniq koordinatalari ( burchak nuqtalari) S. Maqsad funksiyasi P ni har bir tepada baholang Maksimal (agar u mavjud bo'lsa) cho'qqidagi P ning eng katta qiymatidir. Minimal - cho'qqidagi P ning eng kichik qiymati.
Keyinchalik, LPPni hal qilish usullari qanday?
Chiziqli dasturlash masalalarini echishning grafik usuli
- Tavsiya etilgan videolar.
- 1-qadam: LP (Chiziqli dasturlash) muammosini shakllantirish.
- 2-qadam: Grafikni tuzing va cheklash chiziqlarini chizing.
- 3-qadam: Har bir cheklov chizig'ining haqiqiy tomonini aniqlang.
- 4-qadam: Mumkin yechim hududini aniqlang.
- 5-qadam: Grafikda maqsad funksiyasini chizing.
- 6-qadam: Optimal nuqtani toping.
Chiziqli dasturlashda algebraik usul nima? Algebra va Simpleks Usul . A chiziqli dasturlash muammosi (LP) an optimallashtirish muammosi barcha o'zgaruvchilar uzluksiz bo'lsa, maqsad a chiziqli (qaror o'zgaruvchilarga nisbatan) funktsiyasi, va amalga oshirilishi mumkin bo'lgan mintaqa cheklangan sonlar bilan aniqlanadi. chiziqli tengsizliklar yoki tenglamalar.
Bu erda chiziqli dasturlashda burchak nuqtalarini qanday hisoblash mumkin?
The burchak nuqtalari amalga oshirish mumkin bo'lgan mintaqaning uchlari. Siz tizimning grafigiga ega bo'lganingizdan so'ng chiziqli tengsizliklar, keyin siz grafikni ko'rib, qaerda ekanligini osongina aytishingiz mumkin burchak nuqtalari bor. Siz tizimni hal qilishingiz kerak bo'lishi mumkin chiziqli ga tenglamalar toping ning ba'zi koordinatalari ball o'rtasida.
Burchak nuqtasini hal qilish usuli qanday?
The burchak nuqtasini hal qilish usuli to'rtta asosiy bosqichdan iborat:: Har bir cho'qqining koordinatalarini aniqlang ( burchak nuqtasi ) mumkin bo'lgan hudud.: Har birida maqsad funksiyasining qiymatini hisoblang burchak nuqtasi .: Maqsad funksiyasini maksimal qiymat bilan belgilang.
Tavsiya:
Chiziqli tenglamalar tizimini grafik usulda qanday yechish mumkin?

Chiziqli tenglamalar sistemasini grafik usulda yechish uchun ikkala tenglamaning grafigini bir xil koordinatalar tizimida tuzamiz. Tizimning yechimi ikkita chiziq kesishgan nuqtada bo'ladi. Ikkala chiziq (-3, -4) da kesishadi, bu tenglamalar tizimining echimi hisoblanadi
Chiziqli tengsizliklar va chiziqli tenglamalarni yechish qanday o'xshash?

Chiziqli tengsizliklarni yechish chiziqli tenglamalarni yechishga juda o‘xshaydi. Asosiy farq shundaki, siz manfiy songa bo'lish yoki ko'paytirishda tengsizlik belgisini aylantirasiz. Chiziqli tengsizliklarni grafikda ko'rsatishda yana bir nechta farqlar mavjud. Soyalangan qism chiziqli tengsizlik to'g'ri bo'lgan qiymatlarni o'z ichiga oladi
Chiziqli tengsizlik tenglamasini qanday yechish mumkin?

Uch qadam bor: Tenglamani shunday o'zgartiringki, "y" chap tomonda, qolgan hamma narsa o'ngda. 'y=' chizig'ini chizing (uni y≤ yoki y≥ uchun qattiq chiziq va y uchun kesik chiziq qilib qo'ying) "kattaroq" (y> yoki y≥) uchun chiziq ustidagi yoki chiziq ostidan soya qiling. 'kichikroq' (y< yoki y≤)
Chiziqli tenglamalarni grafik usulda qanday yechish mumkin?

Grafik yechim qo'lda (grafik qog'ozda) yoki grafik kalkulyator yordamida amalga oshirilishi mumkin. Chiziqli tenglamalar sistemasining grafigini tuzish ikkita to‘g‘ri chiziqning grafigini chizish kabi oddiy. Chiziqlar grafigi chizilganda, yechim ikki chiziq kesishgan (x, y) tartiblangan juftlik bo'ladi
Chiziqli ifodalarni qanday yechish mumkin?

Chiziqli tenglamalarni yechish uchun quyidagi faktlardan keng foydalanamiz. Agar a=b bo'lsa, har qanday c uchun a+c=b+c a + c = b + c. Chiziqli tenglamalarni echish jarayoni Agar tenglamada kasrlar bo'lsa, kasrlarni tozalash uchun eng kichik umumiy maxrajdan foydalaning. Tenglamaning ikkala tomonini soddalashtiring
