Video: Sin 120 ning kasrdagi qiymati qanday?
2024 Muallif: Miles Stephen | [email protected]. Oxirgi o'zgartirilgan: 2023-12-15 23:41
Hammamizga ma'lumki sinus qiymati 30, 45, 60, 90, 180 kabi ba'zi burchaklarning. Lekin darajalarda bu gunoh 120 =(✓3)/2. Buning uchun oddiy bosh barmoq qoidasi mavjud. gunoh (90+x)=+cos x (bundan buyon gunoh x ikkinchi kvadrantda musbat.)
Xuddi shunday, gunoh 120 qiymatini qanday topasiz?
Yechim: gunoh 120 ° = gunoh (180° − 120 °) = √3/2. Sin 120 °= gunoh (2×90°-60°)= gunoh (60°)=√3/2.
Bundan tashqari, sin240 nima? 240 daraja uchinchi kvadrantda, bu erda burchakning gunohi salbiy. 240 gradusdan 180 gradusni ayirib, mos yozuvlar burchagi 240-180 = 60 daraja ekanligini ko'rishingiz mumkin. 60 daraja gunohdir. Shuning uchun, gunoh 240 daraja = R^2 SCC da.
Bundan tashqari, radianlarda 120 darajaning gunohi nima?
Muhim burchak xulosasi
| th° | thradianlar | gunoh(th) |
|---|---|---|
| 90° | p/2 | 1 |
| 120° | 2p/3 | √3/2 |
| 135° | 3p/4 | √2/2 |
| 150° | 5p/6 | 1/2 |
Tan 120 ning aniq qiymati qanday?
Javob va tushuntirish: The tanning aniq qiymati ( 120 °) -√(3). beri sarg'ish ( 120 °) = sarg'ish (2 × 60 °), biz tangens ikki burchakli identifikatsiyadan foydalanishimiz mumkin
Tavsiya:
Kasrdagi 3/8 ning yarmi nechaga teng?
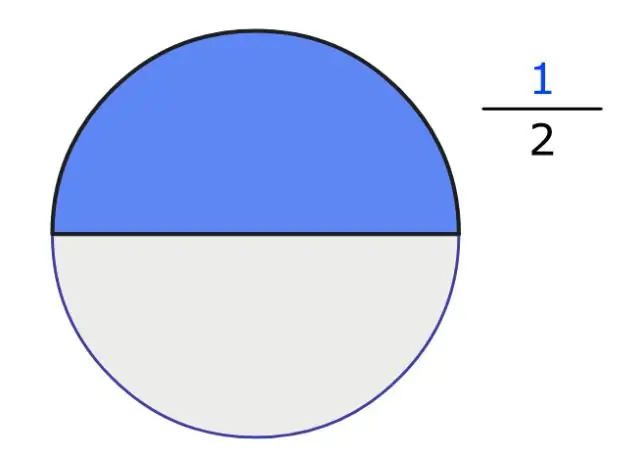
3/8 ning yarmi oddiygina (1/2)×(3/8)
Sin 120 ning aniq qiymati qanday?
Sin120 qiymati √3/2. Chunki u gunohning qiymati har doim ijobiy bo'lgan ikkinchi kvadrantda joylashgan sin (90+x) sifatida bo'linishi mumkin, shuning uchun u kosxga aylanadi. Demak, savolga javob √3/2. Sin (90+x) va Sin (180-x) usuli bilan ham qila olamiz
Kasrdagi 3/4 ning yarmi nima?
Siz kasrning "yarmi" ni maxrajni ikki barobarga oshirish orqali hisoblashingiz mumkin (pastki raqam * 2), shuning uchun 3/4 ning yarmi 3/8 (formula: a/b ning yarmi a/(b*2) bilan bir xil), masalan, 3/4 ning yarmi 3/(4*2) ga teng, bu 3/8 ga teng). Muqobil usul - hisoblagichni yarmiga qisqartirish (yuqori raqam 2 ga bo'linadi)
Sin 5pi 12 ning aniq qiymati qanday?
Javob va tushuntirish: Buning uchun pi r Aniq javob 0,02284431908 deb faraz qilamiz. Yechimni chiqarish uchun avval qavslar ichiga olingan elementlarni yechishimiz kerak. Buning uchun biz pi ni matematik konstantaga tegishli deb faraz qilamiz π π
N ning har bir qiymati uchun L ning qanday qiymatlari mumkin?
Pastki qobiqlar. Orbital burchakli l sonining qiymatlari sonidan asosiy elektron qavatdagi pastki qavatlar sonini aniqlash uchun ham foydalanish mumkin: n = 1,l= 0 bo'lganda (l bitta qiymatni oladi va shuning uchun faqat bitta pastki qavat bo'lishi mumkin) n = 2 bo'lganda. , l= 0, 1 (ikkita qiymatni oladi va shuning uchun ikkita mumkin bo'lgan pastki qobiq mavjud)